Maths in many shapes and sizes

Mathematics is all around us, in the size of things, in the relationship or ratio of things and quantities of things, in the chance or probability of things happening, in the shapes and angles we see, even in our Wesley lion. Lanella Sweet explains howWes the lion has helped students explore measurement, angles, lines, points, shapes, space, perimeter and circumference, area, volume and pi.

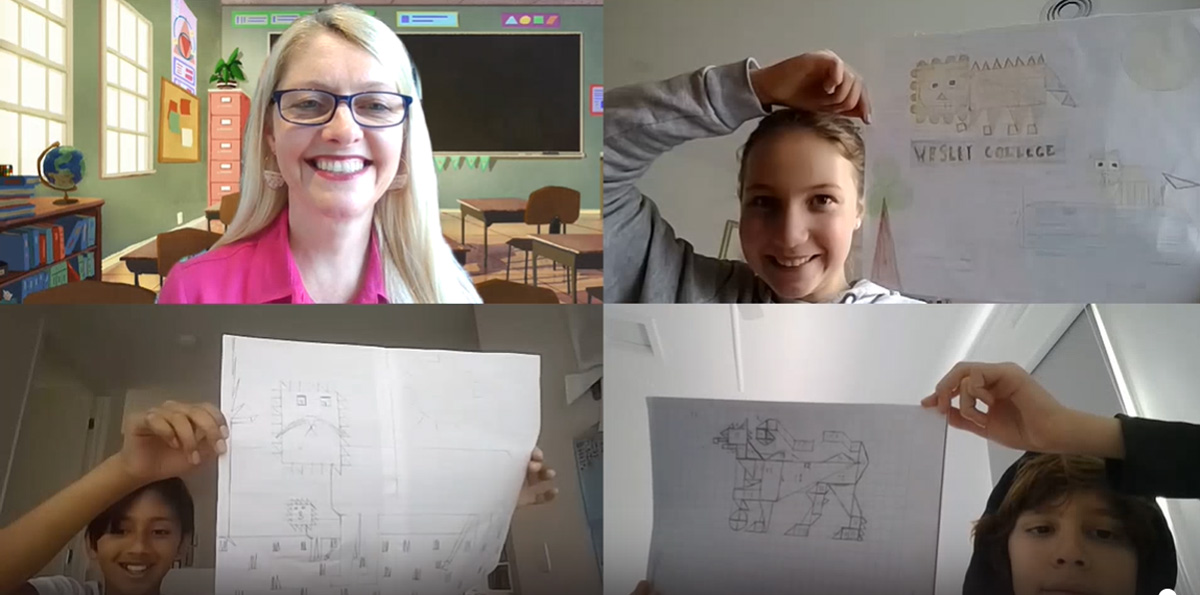
Image above: Year 6 students, clockwise from top right, Mareli Opperman, Matthew Rebelo and Aarav Agarwal, have been using maths to explore a familiar shape, the Wesley lion, with their teacher, Lanella Sweet

Some of our Year 6 students have been exploring shapes in terms of geometry and algebra, investigating graphing, measurement, angles, area, perimeter and circumference, and plenty of problem solving. That exploration has led to an open-ended, guided mathematical investigation with a focus on Wes the lion.

The Wesley lion: a familiar but decidedly irregular and composite shape

Could the students use their mathematical understanding to ‘mathematically design’ Wes the lion, a familiar but decidedly irregular composite shape? With their understandings, the students explored different ways to find unknown values for angles within triangles and quadrilaterals, and ways to use their measurement and classifying skills. They started by drawing simple shapes and combining these, demonstrating they could translate their knowledge into this new context. Constructing geometrical diagrams according to their knowledge of properties demonstrated a range of mathematical skills, concepts and understandings.

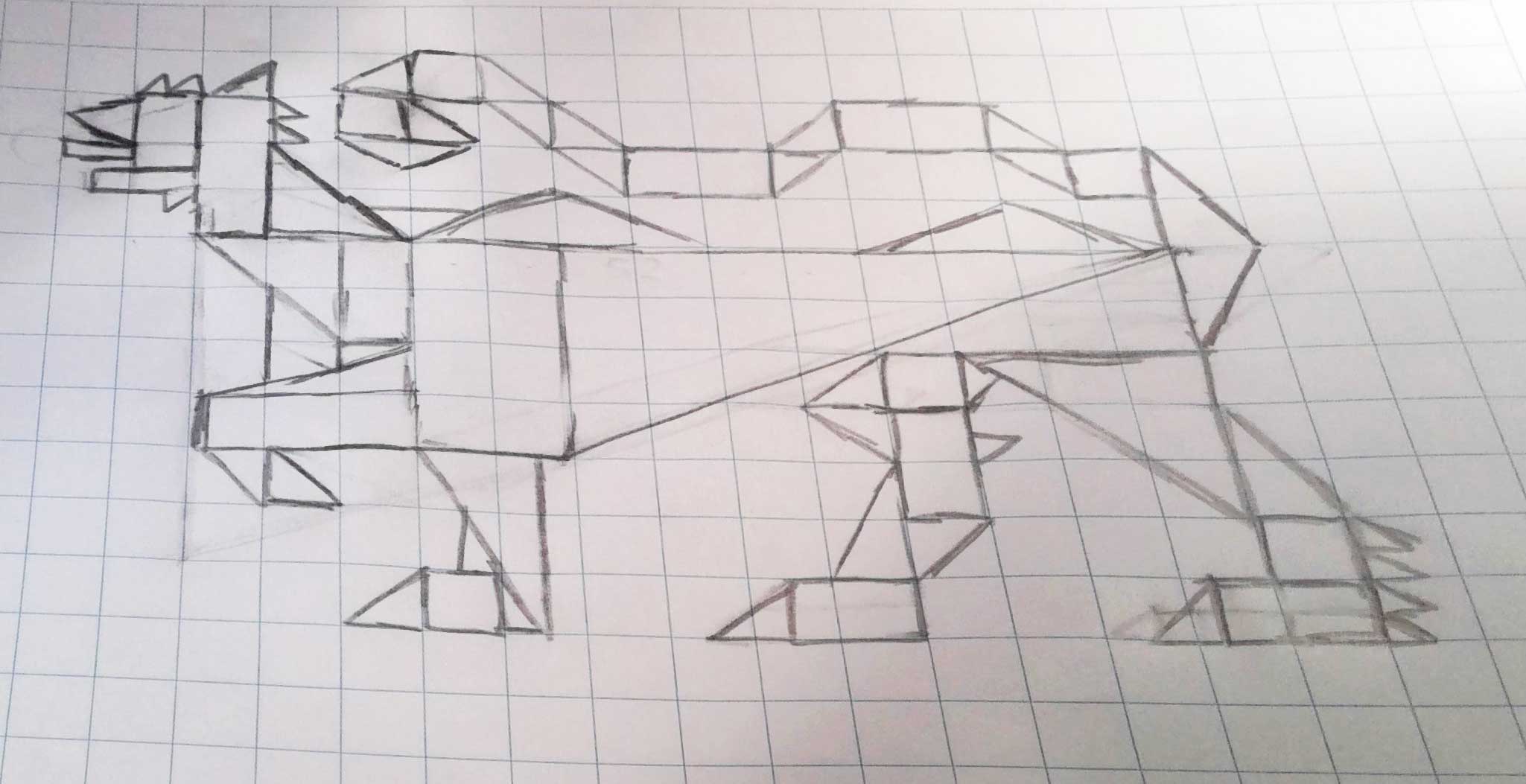
An early step to ‘mathematically design’ Wes the lion by Year 6 student Matthew Rebelo: ‘I like converting what I see into angles and shapes to form the Wesley lion and apply my maths knowledge about measurement and algebra’

Then the mathematical creative design began. The investigation involved demonstrating previously learned content, but also practising, refining and improving with feedback. The creative problem-solving process enabled the students to use their mathematical knowledge and skills in classifying, comparing, explaining, arranging, constructing, calculating, solving, and making hypothesise and generalisations. They were, in the words of Kaye Stacey in Strategies for Problem Solving, expert problem solvers because they, ‘constantly monitor(ed) their thinking, evaluating ideas, checking their progress and keeping their work in line with the original goal.’

Open ended but also structured

Because the mathematical creative design problem was open ended, it was important to develop specific guidelines in collaboration with the students, so they understood the goals of this inquiry, and a checklist and questions to be addressed so they knew what they should record and report in order to demonstrate their proficiencies, processes and understandings.

The questions were framed to encourage the students to drill down to their deep understanding, from connecting basic ideas down to really thinking about representations, calculations and interpretations. Establishing specific parameters really pushed them to work outside their comfort zone and stretch the boundaries of their higher-order thinking.

Truly independent mathematical investigations

A combination of explicit academic outcomes with choice for presenting findings meant the students were able to pursue truly independent mathematical investigations, enriched the curriculum for the students, a point Carol Tieso makes in ‘Through the looking glass.’

Year 6 student Mareli Opperman’s calculations for the area of irregular shapes that approximate the shape of the Wesley lion

One student decided that Wes’s tail might incorporate a multitude of shapes, demonstrating an understanding of classification using triangles from right-angled to scalene. Another used algebra to design triangles and quadrilaterals, with known and unknown values. Another incorporated negative space to calculate the area of irregular shapes. Another investigated using a single curve omitted from a 1cm grid to calculate the perimeter and area of the tail.

The students were able to demonstrate knowledge of geometry and understandings of parallel lines, perpendicular lines, points of intersection and supplementary and complementary angles, as well as features of other shapes, angles, measurements and geometry, and when to apply formulas in order to calculate circumference of a circle and perimeter of rectangle.

How to solve it

There were many problem-solving techniques the students used in their investigations as they moved fluidly between the steps in George Polya’s four-step model for problem solving:

• understanding the problem
• devising a plan
• carrying out the plan, and
• looking back.

They used their knowledge obtained from previous attempts and trials to continue toward their goal of finding the most appropriate solution. And they drew on their prior knowledge, skills and tools, unpacking and understanding the necessary steps to reach their goal in demonstrating mathematical knowledge.

Jinfa Cai and Michael Brook elaborated on Polya’s ‘looking back’ concept, identifying three approaches within this final step:

• generating, analysing and comparing alternative solutions,
• posing new problems, and
• making generalisations.

The students were evidently doing all three, articulating their new knowledge and making links to what they previously knew and how they can transfer to make generalisations and pose new problems.

What do students say?

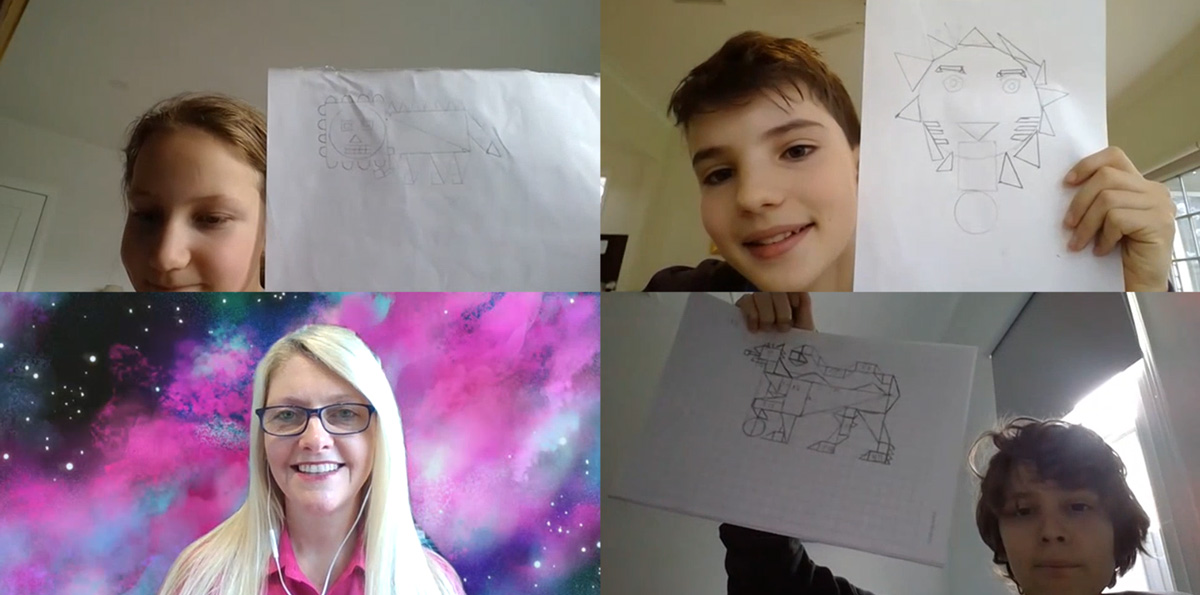
Lions multiplied by three equals a pride: Year 6 students, clockwise from top left, Mareli Opperman, Campbell Holtham and Matthew Rebelo share their early thinking with teacher Lanella Sweet and each other

‘It gives you the opportunity to break a common image into smaller parts and then find the true value of that image (mathematically).’ Matthew Rebelo said. ‘I like converting what I see into angles and shapes to form the Wesley lion and apply my maths knowledge about measurement and algebra. The creating of the picture is fun, and you still get to calculate and think mathematically about things like area and use maths formulas which is quite enjoyable – two good things in one.’

Common to the feedback from all the students is the significant effect of applying their knowledge and skills. ‘I love learning new things and then being able to apply my knowledge into something that I like, and I look forward to every session,’ Campbell Holtham said.

For Fahiz Deen Mohamed, the joy is also in the application. ‘I can now apply maths using my knowledge of triangles, shapes, angles and area, perimeter, which we have learnt,’ he said. ‘Applying this is a fun way whilst being able to fluently understand all the things we have learnt in one.’

Aarav Agarwal agreed. ‘Being able to apply maths to something that is real makes it much more  meaningful and it’s also fun!’ he said.

And for me? It was exciting for me to see the students take complete ownership of their learning, While Wes the lion brought a little bit of Wesley back into our hearts and homes during remote learning and teaching.

Lanella Sweet is an enrichment teacher at Wesley’s Elsternwick Campus.